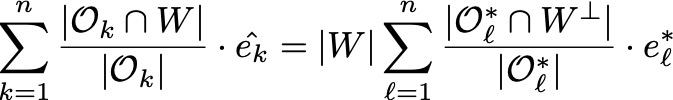指数和の計算と素数の分布

下にある数式は、何年か前に研究中に発見した式です。式の左辺にある$\hat{e_k}$が知りたいもので、それらがみたす関係式です。この式がさまざまなWに対して成立するので、Wを変えていくつも式を立てると、連立一次方程式を解くことで、個々の$\hat{e_k}$が求まります。

$\hat{e_k}$は「指数和」とよばれる和の一種です。それまでは和の定義から直接カリカリと$\hat{e_k}$を計算していましたが、この式を使うと、複雑でとても計算できそうになかった場合まで、簡単に$\hat{e_k}$を求められるようになりました。

この式は、分かってしまえば証明も簡単です。でも、見つけるのには時間がかかりました。たまたまうまく$\hat{e_k}$が計算できたことが何度かあって、 何が起きているのだろう、原理のようなものがあるだろうか、と繰り返しあれこれと考え、紆余曲折を経てたどり着きました。 最終的に綺麗な式にまとめることができたことが、嬉しかったです。

私は整数論を研究しています。この指数和$\hat{e_k}$の値を使って、素数の分布について新たな定理を証明しました。素数の分布は、双子素数の問題など難問も多いのですが、問題が多様で面白く、研究者をひきつけています。 今回は3次方程式および4次方程式の判別式で、「概素数」になるものがたくさん存在することを証明することができました。

指数和$\hat{e_k}$が簡単に求められるようになったと書いたのですが、実はこの式にも限界があって、一定以上複雑な場合は$\hat{e_k}$を求めることができません。
今は$\hat{e_k}$の値がケースバイケースに一定数求められている状況です。その値に規則性を発見することで、もっと難しい場合にも値を求められるようにならないか、考えているところです。