L関数の特殊値の研究

数学科・数学専攻　代数学教育研究分野　森本　和輝 講師

　「3以上の整数nに対して、xⁿ+yⁿ=zⁿを満たす正の整数の組（x, y, z）は存在しない」。この問題はフェルマーの最終定理と呼ばれ、1994年にA. Wiles氏によって証明されるまで360年もの時間を要しました。

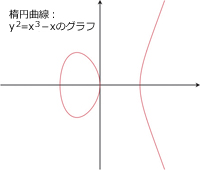
　Wilesの証明の要点は「幾何学的対象」と「解析学的対象」との間の“良い” 対応の存在でした。幾何学とは、図形や空間の性質を調べる分野ですが、その中でも楕円曲線と呼ばれる曲線がこの「幾何学的対象」です。一方で、解析学とは関数の振る舞いを調べる分野で、楕円モジュラー形式と呼ばれる関数が「解析学的対象」にあたります。全く異なる二つの分野の間の対応がこの素晴らしい結果をもたらしたのです。

　この二つの対象を繋ぐ役割を果たしているのがL関数と呼ばれる関数です。L関数は単なるつなぎ目というだけではなく、その性質から様々な幾何学的・解析学的な結果が得られます。例えば、与えられた楕円曲線のL関数の1での値がゼロでなければ、その楕円曲線の中には座標が有理数になる点が有限個しかありません。

　私は楕円モジュラー形式の一般化である保型形式について、そのL関数の特殊値を研究しています。L関数の定義は複雑で、与えられた点での値がゼロなのかどうかも簡単にはわかりません。そこで、周期と呼ばれる保型形式の積分を使って特殊値を表すことで、その性質を調べています。最近の研究では、Siegelモジュラー形式と呼ばれる保型形式に対して、周期とL函数の中心値とを結ぶ公式を証明することができました。

　Siegelモジュラー形式は楕円モジュラー形式の場合のように、Abel曲面という幾何学的対象との対応が予想されており、今後のAbel曲面の研究、また数論的研究にこの公式が役立つことを期待しています。

研究トピックス一覧