Fano多様体とCalabi-Yau多様体の分類

数学科・数学専攻　代数学教育研究分野　佐野　太郎 准教授

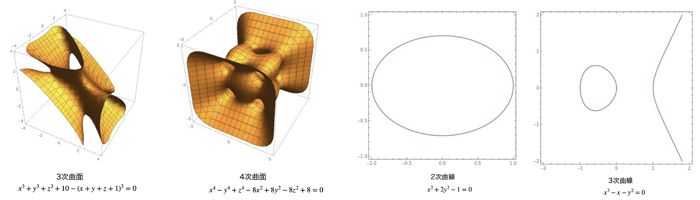
　高校の数学で放物線や円、球面などの図形を習います。例えば円はx²+y²-1=0、球面はx²+y²+z²-1=0という式で定義されます。このように幾つかの多項式が0になるという条件で定義される図形は「代数多様体」と呼ばれます。

　17世紀にデカルトが座標平面を考えて以来、代数多様体は多くの研究がなされてきました。目標の一つとして「全ての代数多様体の分類」があります。座標平面内の2次曲線や3次曲線の分類は古典的ですが、3次元以上の空間に入った曲線の分類は完全には出来ていません。球面など図形自体が2次元以上になると代数多様体の種類は膨大で、現在でも分類の目処は立ちません。

　代数多様体の分類において、Fano多様体、Calabi-Yau多様体、一般型多様体、という3つの「核」が重要です。Fano多様体は2次曲線や3次曲面などを含む比較的理解しやすい対象で、3次元Fano多様体は1980年代に105種類に分類されました。Calabi-Yau多様体は3次曲線や4次曲面を含み、3次元でも分類は未完成ですが、数論や数理物理など幅広い分野との関連もあり魅力的です。私はこれまで「Fano多様体の変形」を主に研究してきましたが、最近は「Calabi-Yau多様体の種類の数は有限か？」という問題にも興味を持ち研究しています。代数多様体は他にも微分幾何や可積分系、また暗号理論など他分野との関連もあり、話題には事欠きません。

研究トピックス一覧